Core Math
Students need to memorize single-digit number facts and learn standard algorithms from the get-go (1st grade), not reform math pedagogy. The aim of learning core math is competency, i.e., the automaticity of foundational factual and procedural knowledge in long-term memory. Kids need to drill to improve skills. W. Stephen Wilson, a mathematics professor who holds a Ph.D. from MIT, writes, "The foundation for K-12 mathematics is laid in the early years of elementary school. [For students] to succeed in college, this foundation must be solid." It isn't, which is the reason that a massive number of high school graduates end up in remedial math at a community college. The message from Dr. Wilson is that if you want to get to college and do well, then you must learn core arithmetic in elementary school. Therefore, teachers need to teach core math (the fundamentals) beginning in 1st grade. Reform math, which still dominates the teaching of math today especially in many elementary schools, gets you to remedial math at a community college. It is a shock to students who were weaned on calculators, received A's and B's in K-8 reform math, and took wrongly named college prep courses in algebra. Common Core or state standards have not corrected the major pedagogical flaw in American math education. Ask any pianist or gymnast about the critical importance of excellent instruction and energetic practice (drill) to improve skill. The same is true for math.
Common Core mentions but does not define standard algorithms, so I am defining standard algorithms as found in Kaplan GED Test.* The single-digit number facts are not hard to memorize in first grade, and the standard algorithms are easy to learn. "Core elementary school mathematics content is straightforward and focused. The catch is that it must be learned well to progress," writes Professor Wilson. In short, children need to automate core arithmetic. And, by core arithmetic, I do not mean substandard Common Core, which includes most state standards or inferior reform math pedagogy. K-5 core arithmetic includes whole numbers, fractions-decimals-percentages, exponents, and proportions. In elementary school, the core math students must also learn parts of algebra, measurement, and geometry. (Let me make clear that the partial quotient method is not the standard algorithm for long division.)
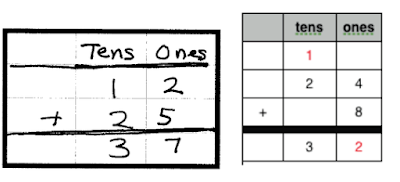
The standard algorithm starts in 1st grade with the memorization of single-digit math facts. Below (12 + 25) shows the practicing of n+2 facts without carrying. The standard algorithm organizes the place value for students. Addition with carrying comes next. The place value idea is to add ones to ones, tens to tens, etc. Also, ten ones make one ten (10), and ten tens make one hundred (100), etc. Numbers are broken down by place value. Dr. Wilson writes, "The place value system is, indeed, mathematics! You cannot teach mathematics without the place value system, standard algorithms, and our other building blocks." Note: In 24 + 8, the 4 and 8 make 12ones, but the "12ones" break down to 1ten+2ones (place value system). The 1ten is carried to the tens column to add tens to tens. See 12.
 |
| The Standard Algorithm First Grade: 1st Marking Period Without Carrying --> With Carrying Single-digit number facts must be memorized. The meaning of numbers is through place value: 37 is 3tens+7ones. Students need to drill to improve skill. |
The problem I see is that students lack competence in core arithmetic, starting with single-digit number facts, which must be memorized (automated), used continually, and reviewed regularly. The standard algorithm is one of the best ways for students to practice number facts. Indeed, students need to drill to improve skill. Also, the standard algorithm organizes the place value system. Indeed, standard algorithms are the best models for place value. Even mathematicians as children drilled to improve skills in the core arithmetic such as number facts and standard algorithms.
The alternative strategies (algorithms) of reform math, which I call pretend arithmetic and mathematician W. Stephen Wilson calls pre-arithmetic, have been ineffective in the teaching of core arithmetic. In my view, the alternative strategies are "extras" that crowd the curriculum and overload students’ working memory. They are not needed and do not lead smoothly to the standard algorithms, which children must master to get to algebra by middle school.
"Mathematics developed incrementally over millennia by geniuses," writes Dr. Wayne Bishop. Children are novices, not geniuses. Asking children to discover math or invent algorithms (e.g., constructivist pedagogy of reform math) is an "absurd pedagogy." In my mind, the use of calculators in American classrooms has hindered achievement. In stark contrast to American teaching, the students in the East Asian (high achieving) nations seldom use technology in their classrooms. It is "conspicuously absent."
Even though reform math's constructivist pedagogy has been promoted by schools of education and supported by organizations such as the National Council of Teachers of Mathematics (NCTM) and the National Science Foundation (NSF), which selected reform math programs as exemplary, it has failed and has led to remedial math at a community college--not college readiness. Not only is constructivist pedagogy inferior, but it also conflicts with the cognitive science of learning. Moreover, researchers Kirschner, Sweller and Clark (2006)** point out that discovery learning and other popular minimal guidance teaching methods are not the best way for students to learn basic math. Over the years, millions of kids have suffered the consequences of constructivist pedagogy.
©2017 LT/ThinkAlgebra
* Kaplan GED Test, 2015 Mathematical Reasoning Prep
Note: I do not approve of using calculators on the GED, SAT, ACT, or any standardized or state test.
** Kirschner, Sweller and Clark (2006): Why Minimal Guidance During Instruction Does Not Work: An Analysis of the Failure of Constructivist, Discovery, Problem-Based, Experiential, and Inquiry-Based Teaching
