Science

Science doesn't prove things right.
It is a method that eliminates wrong ideas.
Correlation should not imply causation. 

Sense Gravity! 
"Scientists think that the force of gravity may be carried by a particle called a graviton. The existence of gravitons has not yet been confirmed experimentally." We may never find a graviton.

Scientists believe electrons and quarks exist even though they have never seen them. 

Note. This page replaces the Science page on ThinkAlgebra.org.

Einstein based his theories of relativity on two assumptions: "It’s impossible to exceed the speed of light; it’s impossible to tell the difference between gravity and acceleration." (Quote: QuantaMagazine, 2021) If either of these assertions were not true, the laws of physics would be rewritten. Physics is the most fundamental science, yet it is downplayed in the NextGen science standards. 

John Horgan ("The Paradox of Karl Popper," Scientific American) writes, The lesson of quantum mechanics and even of classical physics, Popper said, is that nothing is determined, nothing is certain, nothing is completely predictable; there are only “propensities” for certain things to occur." "We don't teach this idea in our science classes. 

What about Charles Darwin's theory of evolution? 

Suddenly Popper pounded the table and exclaimed, “one ought to look for alternative theories!”

Elementary school students often lack proper science education. Math is lacking in elementary school science. For example, K-5 students are not taught atomic structure and energy levels, the relationship between magnetism and electricity, forces and motion (Newton), speed and velocity, weight and mass, and calculations for average speed and acceleration. Also, they seldom learn the difference between physical and chemical changes. And the list goes on and on. These are important concepts in physics but are often ignored. Why is that?   

There is misinformation coming from sources such as The National Academic of Sciences, Engineering, and Medicine. "The amount (weight) of matter is conserved when it changes form, even in transitions in which it seems to vanish (e.g., sugar in solution, evaporation in a closed container)." It is not "weight." It is mass. Secondly, we know that mass is not conserved, but energy is. 

Students are not taught the difference between observation and inference to foster clear thinking. Moreover, children are not learning math skills, including algebra, such as linear functions, needed to do and grasp science. In science, as in math, knowledge counts a lot! Unfortunately, much of science in K-5 has been reduced to disjoint hands-on activities. Teachers seem to skip over the knowledge part, so students learn very little science. 

Today, we are told that the best way to learn science is hands-on, but I'm afraid I have to disagree. As we used to call them, hands-on or labs should be directly related to the science the student is studying in class. The problem is that often they are not. If the students were studying and exploring Newton's 3rd Law in class, then I think the hands-on activity of rockets would not only be fitting but fun as well. Thus hands-on activities should be an extension of, and reinforcement of the content learned in class, which includes reading the textbook and paying attention in class when the laws are discussed, examined, and applied by a teacher who uses explicit instruction. In short, hands-on activities should not be a substitute for learning scientific knowledge. Hands-on activities should promote the scientific content the student is currently studying.   

Often, the same set of observations or measurements can be interpreted in several different ways. Thus, inferences or conclusions may vary considerably. It is also the reason that scientific theories are not set in stone. New observations can fine-tune or change a theory. Science is not perfect, but math is. 

Most kids are not proficient in science (NAEP). 
For example, only 22% of 12th-grade students are proficient or above in science, and only 2% are at the Advanced Level. Most kids are not skilled in science, to me, means that most students know very little content, which is the crux of the problem. In my view, the new science Framework (NextGen) from the National Research Council (July 19, 2011) downplays content knowledge. The framework aligns well with hands-on inquiry methods. In short, kids are not required to learn a lot of science content. The background knowledge is essential but skipped. 

Note. Reformers assert that the best way (or the only way) for young children to learn science is through hands-on, discovery, or inquiry methods. It is nonsense. 

Furthermore, students lack the background knowledge and the math needed to do the science, so it follows that they would have difficulty explaining the experiments' results. I cannot overemphasize the importance of knowledge in science. The stress in science education has shifted to mostly process, but process fizzles out fast without learning adequate content. I am not a fan of programs that do not focus on content knowledge. Thinking without content knowledge is empty. 

Read Science to Learn Science
Children need more than hands-on stuff; they need to read science to learn science from good textbooks. Experiments should be done to reinforce the content students are currently learning. Also, students need to learn science vocabulary. 

7th-grade student reading her physical science textbook.

Dr. Mark A. McDaniel says that before engaging students in inquiry-based problem-solving in science or mathematics, they should have a sound knowledge base (background knowledge). In short, background knowledge of fundamentals in long-term memory is key to problem-solving in math, science, and other academic disciplines. Furthermore, background knowledge is domain-specific. To learn math or science well takes plenty of effort, study, and hard work. 

Kids need to do more than observing single-celled paramecium swimming around under the microscope. It's intriguing, but they should also learn background knowledge such as the cell theory, the structural differences between plant and animal cells, the organelles in cells, and what each does. Also, the nucleus and the code for genetic information (DNA), mitochondria, chloroplasts, cellular transport (diffusion/osmosis), glucose to ATP, photosynthesis, amino acids and proteins, enzymes, cell division (mitosis), and so on. Lastly, lab work (hands-on science activities in small groups) should reinforce the topics students are currently studying. 

Observing unicellular protists under the microscope is a lot of fun. Still, students should also study the background knowledge, such as the parts of a single-celled paramecium, the structural differences between animal and plant cells, the organelles' functions, and so on. Students should learn science vocabulary. They need excellent science textbooks.

Pond water is teaming with protists.

I cannot overemphasize the importance of learning content knowledge in science. The stress in science education has shifted to mostly process, but process fizzles out fast without learning adequate content. 

So-called experts argue that hands-on inquiry group work should be the primary method of learning science. The new science standards stress process over content knowledge. But, this method is inefficient and backward. Students would learn much more science by reading science textbooks and listening to presentations (explanations) given by knowledgeable teachers in class. The hands-on inquiry labs should reinforce the content, not replace it.

Click: The New (NextGen) Science Framework

Even though I wrote this a few years ago, it demonstrates that the new science standards' primary focus is the processes, not content knowledge. I see the same trend in math and reading: process over content. It's backward. 

Note. Students don't read books anymore. They should! 

Many people think that if you make a bunch of observations, you make up a rule, idea, or theory, but that's not how real science works. If you are an expert in a field, you guess a rule (Feynman), then carefully craft an experiment to make observations (measurements) to test it. Also, experiments should be replicated by other scientists and peer-reviewed. Intrinsically, real science eventually weeds out bad ideas. On the other hand, research in education doesn't do that. Usually, there is no repeatability. Finding a control group is next to impossible. Consequently, many unsupported ideas, practices, or theories in education still thrive today.

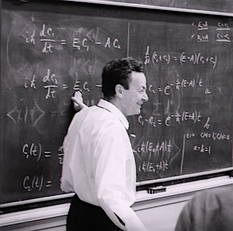Feynman at Caltech - "You don't know anything until you have practiced."

"In education, you increase differences."
Richard P. Feynman was invited to a conference to discuss "the ethics of equality in education." He confronted the experts by asking this question. "In education, you increase differences. If someone's good at something, you try to develop his ability, which results in differences or inequalities. So if education increases inequality, is this ethical?" (Surely You're Joking, Mr. Feynman! by Richard P. Feynman, Nobel Prize in Physics)

​"You don't know anything until you have practiced." (Feynman)

Atoms and molecules exist, move, and bounce off each other. (Einstein, 1905)

Photo Caption: How can one drop of green food coloring make the water uniformly green? Einstein:  Atoms exist, move, and collide!

Be Skeptical!
Richard Feynman exhorted citizens to be skeptical of claims and only believe what could be tested.

Many studies show associations (i.e., correlations), but a correlation is not causation or fact. Guy P. Harrison (Think) writes, "The brutal truth is that human brains do a poor job of separating truth from fiction. It leads to many false beliefs. Think like a scientist. Proof comes before belief." Sometimes, what some scientists say and what science shows is not the same.
 

© 2018-2019, 2020 LT/ThinkAlgebra.org

Model Credit: GabbyB,  Katherine,  HannahE, CalTech
Major Changes: 7-13-19, 7-16-19, 7-19-19, 7-27-19, 11-21-19, 11-22-19, 12-23-19, 11-4-2020

Pre-Arithmetic Skills

Kindergarten

Pre-Arithmetic Skills

When learning arithmetic, students should start with simple skills. For example, in Kindergarten, students should count and write numbers daily, repeatedly do simple arithmetic combinations on a number line, such as 2 + 7 = 9, and use an equal arm balance to measure masses of objects. Other pre-arithmetic skills include the commutative rule (2 + 3 = 3 + 2), adding zero (6 + 0 = 2), adding one (11 + 1 = 12. “The beginning exercises are simple and do not resemble later exercises (just as beginning piano exercises do not look much-advanced ones). 

On the number line, start with simple sequences of calculations: 

1 + 1 = 2, 1 + 2 = 3, 1 + 3 = 4, 1 + 4 = 5 Or 5 + 1 = 6, 6 + 1 = 7, 7 + 1 = 8, etc. OR 5 + 1 = 6, 5 + 2 = 7, 5 + 3 = 8, 5 + 4 = 9, etc. Do this rote training on the number line, again and again. When introducing larger numbers such as the teens, students should learn them as eleven: 10 +1; twelve: 10 + 2, etc. on the number line that goes from 0 to 20. 

Also, K-students should learn to read using Zig Engelmann’s book (Teach Your Child to Read in 100 Easy Lessons).

Engelmann: "Only 10% of each lesson is new material. The remaining 90% of each lesson’s content is review and application of skills students have already learned but need practice with in order to master."

Teach Kids Algebra (LT)

I do not teach to the state test. I give lessons on pre-algebra skills, which puts stress on a student's cognitive effort. It's sensible but not always well received by some students who don’t want to think.  

Also, the school should abandon reform math and return to teaching basics—memorizing number facts, practicing the standard algorithms for mastery, recognizing patterns, and solving word problems by writing and solving equations. The problem is that the teachers don’t know how to teach math basics. Their skills are weak. They don’t know how to teach for mastery. They are told to teach the test, which is a “ bits and pieces” curriculum.    

In the reform math era, students are confused, and parents are baffled. Reform math stresses strategies, alternative algorithms, so-called mathematical practice standards, group work, and other extras,  Students are novices, not little mathematicians. They don’t think like adults. Novices require explicit instruction and a lot of repetition, practice, and review to learn something like arithmetic.  

We sent men to the moon using Newton’s Laws, a slide rule, and trig; today we send students to remedial math at community colleges using calculators and reform math. Even the state tests and the GED, AP, and SAT exams require calculators. Students are weak in arithmetic and don't know enough algebra. A whopping 87% of TUSD high school graduates who apply at Pima Community College (Tucson) are placed in remedial math classes. The math curriculum in Tucson and Arizona is not world-class. This is the case in most states. Common Core math is not world-class.   

There is no generalized thinking skill independent of domain content knowledge (E. D. Hirsch). But, many educators believe that there is a generalized thinking skill that can be applied to anything. It simply isn't true. Problem-solving (i.e., critical thinking) is domain-specific. Thinking in math is different from thinking in science, and so on.

Also, “understanding" does not produce mastery; practice does. Even our best students are below international benchmarks. "It's not that Asian kids overachieve; it's that American kids underachieve!" We should focus on the mastery of fundamentals like Singapore, not “learning” for a state test. But, we don’t. 

The way we teach math can block a child’s future. 

For decades, we have taught arithmetic poorly.  

The math I taught to 3rd graders in the early 70s was far different from what 3rd graders learn today. Today, students can’t calculate well, even though it is a key factor for problem-solving. You don't make drawings to do arithmetic. Who does that? It's another bad idea! Students should rely on memorized facts, fast algorithms, and pattern recognition to solve math problems. 

In general, U.S. Children are not mastering basic arithmetic. They are predominantly taught a version of reform math that downplays memorization, standard algorithms, and traditional instructional methods such as drill-to-develop-skill. Also, “state standards” are based largely on Common Core, regardless of the rhetoric from state leaders. CC math is not world-class, which puts our kids behind.

The main reason for our educational problems is "the teaching" in the classroom, but teachers, educators, and administrators don’t think that way. Educationists give excuses such as poor parenting, societal problems (e.g., poverty, drugs), and not enough money. The same excuses were given 50 years ago. "If we only had more money…."

Even the best students complain that the reform math they are taught is confusing and overly complicated. Reform math is a hodgepodge of strategies and alternatives, not traditional arithmetic. Parents are baffled and can’t help their kids. Reform math is a hodgepodge of strategies and alternatives, not traditional arithmetic. The many alternative algorithms and so-called strategies take precedence over the standard algorithms. 

(Note. I call today's math "reform math," which stems from the 1947 NEA Yearbook and the 1989 NCTM standards. Reform math is promoted in Common Core and state standards and taught in schools of education.) Even in GATE classrooms, students are taught grade-level math, which is actually below grade-level at the international level. Our kids are behind, but no-one takes notice. We keep doing the same things, again and again, hoping for different outcomes that never happen.)

This is the status of many 4th graders. They struggle over the content they should have mastered in 2nd and 3rd grade but had not. Arithmetic isn’t taught for mastery. Memorization and practice-practice-practice and review-review-review have fallen out of favor in the progressive schools across America. Teachers use inefficient minimal-guidance methods and test prep. They are no longer the academic leaders in the classroom; they are facilitators, which is a radical change.

My 3rd Grade: 1971-1972 

In contrast, my 3rd graders (1971-1972), 28 of them, memorized the x-facts and practiced both the multiplication and long-division standard algorithms. They also learned fractions and parts of measurement and geometry. In addition to math, my 3rd graders had lessons in reading/phonics, writing/grammar, science, history, cursive, and so on. All students were expected to use cursive writing starting no later than December for spelling and writing assignments. The 2nd semester was long-division time. Incidentally, addition, subtraction across zeros, and place value were reviewed and extended in the first couple weeks of school. No manipulatives were used. Discipline problems in my classroom did not exist. It was a fun time, but hard work.

My algebra program (Teach Kids Algebra - TKA) has been in decline lately because it is linked to basic arithmetic. Students are not learning enough arithmetic. For example, they don't master multiplication in the 2nd and 3rd grade. The problem will persist as long as teachers focus on strategies and alternative algorithms (aka reform math), and use inefficient minimal-guidance methods (e.g., group work) and test prep instead of the explicit teaching of traditional arithmetic from the get-go (1st grade on up). 

Students need to memorize stuff and practice the standard algorithms starting in the 1st grade. Continual review is needed, too. 

Memorization is good for kids. 

Facts in long-term memory boost thinking and problem-solving in working memory.

Note. I taught and supervised the Talented & Gifted programs (TAG) at five elementary schools when I lived in Delaware. The TAG program was for the academically advanced and had stringent qualifications for admittance.  

The GATE program is mostly an enrichment program for bright students. As implemented at R/N, it is not for advanced math students or acceleration in math. Although some would disagree, GATE is not designed to improve an elementary student's achievement in specific academic areas such as math, reading, or science. Even the students in self-contained GATE classes get grade-level math for equity. Equity, which is a "fallacy of fairness," cannot produce equal outcomes (Thomas Sowell). “Equalizing downward by lowering those at the top is a crazy idea.”  

In contrast to GATE, my algebra program is focused on content. It does not pretend to teach children to be more creative nor does it stifle curiosity. It is not developmentally inappropriate as many believe. However, TKA does require children to use their cognitive abilities, but some bright kids don’t like that. Math is harder than other subjects because it is abstract. I have observed that some very intelligent students are weak in standard arithmetic. 

Another myth is the right brain/left brain. We now know that any cognitive activity goes through both sides of the brain, not favoring one side over the other. Also, there is no evidence for learning styles (Willingham). There are many common practices and theories in education that are not supported by scientific evidence.

Note. Kids aren't reading books this summer. They would rather spend much of their free time playing games, texting, or doing social media (Instagram, etc.) on their smartphones. Kids, today, are glued to screens. 

LT

https://thinkalgebra.org/index.html

©2019 - 2020

Preparing Students for the Future

Preparing Students for the Future!
It is common sense that if kids don't learn the fundamentals of arithmetic, then they are blocked from higher-level math (Engelmann).  The fundamentals start in 1st grade with the meaning of numbers by place value (e.g., 13 is 10 + 3), rules: add zero (3 + 0 = 3), add one (5 + 1 = 6), and commutativity: 3 + 4 = 4 + 3), memorizing the number facts, and learning the mechanics of the standard algorithms, first. Incidentally, the standard addition algorithm is the best model for place value and should be taught in the 1st-marking period of 1st grade. 

Content-free is the wrong approach!
Teachers are instructed to teach higher-level thinking skills (i.e., critical thinking or problem-solving) before kids had mastered the fundamentals that support content thinking. For example, learning basic arithmetic content starts with memorizing the number facts, place value, and practicing the mechanics of the standard algorithms for automaticity. Students should practice and review the basics to make them stick in long-term memory for use in problem-solving. Applying content knowledge is the next significant step. Recognizing problem types is critical in arithmetic and algebra.  

Robert Pondiscio (Fordham Institute) writes, "Hirsch, myself, and many others have long lamented the content-free, skills-driven, curriculum-agnostic brand of schooling that has come to dominate American primary education. This state of affairs is due in part to mistaken notions about how children learn." I do not blame teachers; they are doing what they had been trained to do, but I question "the teaching" itself.  Critical thinking (aka problem-solving) without content is empty. Thought is domain-specific. You cannot solve a trig problem without knowing some trig or translate Latin without knowing some Latin. In math, efficient calculating skills are an intrinsic part of problem-solving. Passing from one grade to the next does not mean the student is competent at grade-level arithmetic. More likely than not, most students are below grade level (NAEP math). It is common sense that if kids don't learn the fundamentals of arithmetic, then they are blocked from higher-level math (Engelmann). So what has happened to common sense? 

Thomas Sowell (Discrimination and Disparities, 2019) points out, "Education is an area in which differences in values and behavior play havoc with policies based on an assumption of sameness. There is no reason whatever to assume that education is valued equally by all individuals or groups."
Some children do not value education or study as much as others. In contrast to Asian families, education is not the highest priority in some American families.

Focus on Content Knowledge

Knowledge has always been the best preparation for the future. You can't apply something that you do not know well in long-term memory. Thought without content knowledge is empty. Indeed, strong academic skills, a work ethic, persistence, postsecondary education, and some "chance" are needed to prepare students for future jobs. Many of today's careers use math. 

Don't Underestimate the Role of Chance
Much of what happens is random. Opportunities can arise suddenly. Thus, in many cases, being at the right place at the right time with the right set of skills can convey opportunities that others may not have or value. It's persistence and chance. We cannot equalize opportunities or balance outcomes. The real world is not Lake Wobegon, in which all the children are above average.     


Leonard Mlodinow (How Randomness Rules Our Lives) writes, "It might seem daunting to think that effort and chance, as much as innate talent, are what count. Our degree of effort [persistence] is up to us." Mlodinow points out that we underestimate the effects of randomness for "successes and failures" in life. Furthermore, he writes, "Ability does not guarantee achievement, nor is achievement proportional to ability."

Kids today, have opportunities in government schools that I never had when I was a student. But, many do not value learning! 

Observation. Some students coming into the 7th grade still don't know the times tables for instant recall and long division, which are skills I used to teach in the 3rd grade for mastery. The primary reason kids don't know arithmetic well enough is the teaching. For decades, kids have been taught reform math, not conventional arithmetic, and it shows on national and international tests. Recently, a 2nd-grade teacher complained to me that kids coming into 2nd grade know absolutely nothing.  

Ashley Berner (Johns Hopkins) points out, "Numerous recent studies suggest that switching from a low- to a high-quality textbook can boost student achievement more than other, more popular, interventions, such as expanding pre-school programs, decreasing class sizes, or offering merit pay to teachers. It is also cost-effective."

Will our kids learn enough math to get into the STEM and math-related fields? Probably Not!

The reality is that academic performance in many U.S. schools has weakened over the decades. We live in an era that marginalizes math instead of valuing it as a basic problem-solving tool. The misguided ideas of progressive reformists do not connect to the real world that is rich in mathematics. There is a lot of lip service given to math, but, in fact, the reformers dodge the main issue in math--the teaching. Pressing keys on a calculator is not knowledge, nor are googling, texting, posting Instagram photos, and so on.

The critical importance of math for the U.S. economy and the future jobs of our children is grossly underestimated in our schools. Only 25% of high-school seniors are proficient in math (NAEP, 2017), but only 3% are at an Advanced Level.  

Unlike American parents, Asian parents push their young children into math, and it shows by 8th grade: 54% of Singapore 8th graders scored at the Advanced Level of TIMSS compared to a scant 10% of U.S. 8th graders. The Advanced Level of TIMSS demonstrates that U.S. math programs are lacking in the content that prepares students for the future. It does not surprise me because the States adopted standards that were primarily Common Core. In short, the math curriculum found in most states is substantially below the content taught in high performing nations. It is not world-class.

For decades, American kids have stumbled over simple arithmetic, which is the foundation for algebra and higher-level mathematics. The widespread progressive math reforms do not work. The curriculum is not world-class, and the progressive methods of teaching are ineffective (inferior). If the children aren't learning, then there is something wrong with the teaching, that is, with the curriculum and the instructional methods. 

We should prepare more students for a solid precalculus course in high school. Also, Algebra-1 is a middle school course for typical students who are prepared. Likewise, calculus is a high school course for average students who are prepared. But, the reform math curriculum and progressive instructional methods, including teaching the state test, have driven underachievement, not preparedness. Being proficient on the state test does not mean your child is college-ready or knows basic arithmetic. 

Progressive reformers hide behind the concept of sameness (i.e., everyone gets the same instruction, regardless of achievement level), which is another inane idea. Sameness is an illusion. Thomas Sowell (Discrimination and Disparities, 2019) points out, "Education is an area in which differences in values and behavior play havoc with policies based on an assumption of sameness. There is no reason whatever to assume that education is valued equally by all individuals or groups."

Progressive ideas litter the education playground. 
For example, an "education" professor claims that teaching kids math discriminates against children of color. How stupid! 
Comment: "Why would anyone think that minorities would be less able to do math than anyone else?"

Rochelle Gutierrez, an education professor, not a mathematician, claims that teaching kids algebra and geometry discriminates against students of color and perpetuates white "unearned privilege." She is dead wrong! Gutierrez is one of a host of left-leaning-ed-radicals who assert that achievement is "privilege." It's not! Her message is clear: Don't Achieve. If you achieve, it is unearned, which is a toxic message for both minorities and whites who are trying to better themselves. 

Contrary to Gutierrez and others like her, achievement in math is earned through hard work, practice/review, and study. Indeed, students of all colors need higher-level math courses to expand their career choices later on.  

Note. How do we prepare children for the jobs of the future? 
We prepare students the same way we have always trained students for the future. Kids need strong academic skills (math, science, reading/vocabulary, writing/language) and a work ethic to get a good job now and in the future. Most students will need some form of postsecondary education or training. Moreover, students should take a lot of math and science in schools, such as precalculus and algebra-based physics.  

For decades, K-5 schools have been weak in both math and science. It carries over through middle school and high school. Unlike Asian nations, we don't push kids into math, and it shows: 54% of Singapore 8th graders scored at the Advanced Math Level compared to only 10% of American 8th graders (TIMSS). If our kids are not good at math, then we made them that way. Moreover, many of our students are not linking the learning of math to future careers and employment. There is a multitude of jobs that use math. 

The bottom line is that all students need to upgrade their math skills to move forward.

The progressive educationists do not take learning math seriously enough. Math education has been beset with problems for decades. For example, State Math standards, which are based primarily on the Common Core, are significantly below world-class standards. So, why were they adopted? Consequently, by the time American kids reach the 4th grade or 5th grade, they are about two years behind their peers from top-performing nations. 

The math gap starts in the 1st grade and grows through the grade levels. For example, Singapore 1st-grade students learn much more basic arithmetic than American children, including multiplication and formal algorithms to add and subtract (i.e., standard algorithms). Also, Singapore 1st-grade students memorize math facts and drill for developing skill.

With some pivotal changes, we could do the same. We could teach for the mastery of fundamentals using explicit teaching and a world-class curriculum, starting in the 1st grade, but we don't. Parents should take the initiative and teach basic arithmetic to their children at home, but will they? Also, the policy of mixing low-achieving math students with high-achieving math students in the same math class has been a recipe for mediocrity. Thomas Sowell explains that "equalizing downward by lowering those at the top is a fallacy of fairness."   

What many teachers don't get is that mathematics is cumulative, starting with arithmetic: one idea builds on another. You can't teach math like you teach social studies. 

In math, the learning of future lessons depends on the mastering of previous lessons: the prerequisites (Gagne). Learning is what students remember later on, not just for a test. Children are not learning basic arithmetic because it is not being taught for mastery. It's the teaching, as the late Zig Engelmann had said, repeatedly. The widespread math reforms have not worked the children aren't learning, then there is something wrong with the teaching, that is, the curriculum and the instructional methods. Some valuable content isn't taught because it is not on the state test. 

But, progressive educationists don't see it that way. They blame permissive parenting, societal ills (poverty, drugs), and insufficient funding. I heard the same arguments 50 years ago. Nothing has changed! Also, educationists claim that higher pay, smaller class size, more group work, and technology-technology-technology (laptops for all, etc.) would magically fix the problem.

Click Use Math
"Everyone has asked themselves: When will I use math? Believe it or not, hundreds of careers use skills learned in high school math on a daily basis." But, learning high school math well (through precalculus) depends on mastering K-8 arithmetic, geometry, and algebra, starting with 1st-grade arithmetic. Students must know the content, but many do not.  

19th-Century? How many middle school students, high school students, or adults?
19th-Century 4th-Grade Basic Arithmetic in America
1. Find the interest of $60 for 4 months, at 5 percent.
2. If 12 peaches are worth 84 apples, and 8 apples are worth 24 plums, how many plums shall I have for 5 peaches?
(Source: Ray's New Intellectual Arithmetic, 1877, which combined 3rd+4th-grade arithmetic into one compact 140-page book.)

Sometimes, learning arithmetic, such as the multiplication table, is not much fun. Children with weak math skills have limited career opportunities later on.  

Also, read the Future.
Knowledge has always been the best preparation for the future, no matter the epoch.

Last update: 7-22-19, 7-29-19, 7-31-19, 8-11-19

©2019 - 2020 LT/ThinkAlgebra