Cogitating on Education
January 20, 2020
I don't make New Year resolutions. Instead, I reflect on education and often quote or paraphrase others who are smarter, more knowledgeable, or wiser than I am.
First, let me say that K-8 classroom teaching is one of the most challenging careers today. If I had to do it over, I think I would be a Latin teacher at a Christian, classical, or private school, not a K-8 math and science teacher in the public schools, because Latin doesn't change. I changed my college major to classical languages, so when I graduated, the public schools needed math and science teachers, not Latin teachers. I had a background in math and science, so later, I became a K-8 math and science teacher, and after I retired, I tutored Algebra-2 with trig, precalculus, and Latin for several years. Also, as a K-8 teacher, I taught most grade levels, including a self-contained 1st-grade class, which was an adventure. Here are some musings about education for 2020. Excuse the repetition. LT
I am astonished at what kids don't know in math.
Arithmetic isn't taught well, not like it used to be. The way reading has been taught isn’t working either. “[A] child who ends the third grade below level in reading will likely never catch up to his peers,” writes Dana Goldstein (The Teacher Wars). States modified the test cut scores or the results so that most kids would pass 3rd-grade reading and not be held back. But, by the next grade level (4th grade), only 35% were proficient or above in reading (NAEP) or math. Only 14% of high school students can distinguish fact from opinion.
Arithmetic isn't taught well, not like it used to be. The way reading has been taught isn’t working either. “[A] child who ends the third grade below level in reading will likely never catch up to his peers,” writes Dana Goldstein (The Teacher Wars). States modified the test cut scores or the results so that most kids would pass 3rd-grade reading and not be held back. But, by the next grade level (4th grade), only 35% were proficient or above in reading (NAEP) or math. Only 14% of high school students can distinguish fact from opinion.
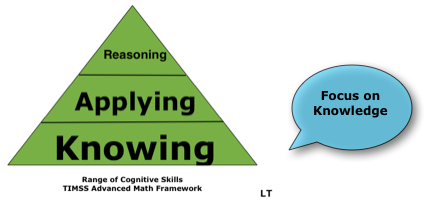
"Factual knowledge must precede skill." By skill, Willingham means upper-level analysis or synthesis, but in the absence of factual knowledge, it is impossible to do that. Teachers want students to learn many different skills, such as critical thinking, but upper-level thinking skills of Bloom's Taxonomy require extensive factual knowledge (Willingham). It is basic cognitive science, but teachers don't get it or weren’t taught it.
Learning math facts may be dull and not much fun, at times, but it is essential, especially in arithmetic starting in the 1st grade. We grossly underestimate the content students can learn at an early age, i.e., in grades 1 to 3, including long-division. Often, more complex content is not taught, such as ideas from algebra, geometry, and measurement, which can append to basic arithmetic. Students should learn content that is above grade-level arithmetic at earlier ages, but first, they need to learn arithmetic.
Learning math facts may be dull and not much fun, at times, but it is essential, especially in arithmetic starting in the 1st grade. We grossly underestimate the content students can learn at an early age, i.e., in grades 1 to 3, including long-division. Often, more complex content is not taught, such as ideas from algebra, geometry, and measurement, which can append to basic arithmetic. Students should learn content that is above grade-level arithmetic at earlier ages, but first, they need to learn arithmetic.
Educators and progressive reformists grossly underestimate the content that students can learn given proper instruction. We seem obsessed with grade level.
Trig in 4th Grade! No tables or calculators.
Kids don't need more strategies, mathematical practices, or a hodgepodge of alternative or invented algorithms; they need a bedrock of knowledge in long-term memory. "Factual knowledge [in mathematics, such as 6 x 9 = 54] must precede skill [e.g., critical thinking, higher-level thinking skills]," writes Willingham. In short, teach facts (i.e., the content) that will enable critical thinking (i.e., problem-solving in math and science).
Jill Barshay for the Hechinger Report summarizes Daniel Willingham's conclusion “that critical thinking skills don't translate from one subject to another but that subject-specific critical thinking skills can be explicitly taught as you go deep into the lesson, be it history or math, as students need to learn a lot of information to process it.” She writes, “In other words, critical thinking is necessary to absorb content better, but a content-rich lesson is needed to teach critical thinking in the first place.” So, start with content-rich lessons. (We don’t have them.)
Cognitive Science Is Great!
Clutter-Clutter-More Clutter
Removing topics as extras (too many topics) such as probability and data analysis in K-8 was one of the goals of the Math Panel (2008). So, what happened? Instead, strategies, mathematical practices, alternative/invented algorithms, which are reform math pedagogy (and leftovers from NCTM math) needlessly clutter the curriculum for novices and marginalize the memorization of math facts and the fast learning of standard algorithms. Kids must memorize math facts and learn standard algorithms from the get-go to advance. This goal--anything considered Old School--was dealt a blow by progressive pedagogy (i.e., equality or "fallacy of fairness"), which became the prevailing vision even if children learned less. There are many terrible ideas in education; this (the "fallacy of fairness by lowering those at the top" Sowell) is but one.
It would be an astonishing feat if we could transform high school students who read and do math at the 6th-grade level into engineers. Since the 70s, most of the funding targeted the bottom kids, leaving the rest in limbo, especially the advanced students. The idea was to get low-achievers into college. It didn't work because they could not read or do math well and ended up in a remedial math rut at community colleges. We cannot magically change low achievers into high performers. The curriculum isn't strong enough. Hush! Some kids just aren’t smart enough or study enough. There are always exceptions.
Students need more knowledge in long-term memory to enable problem-solving, which is domain-specific. In math, practical paper calculating skills that always work are essential knowledge. Why are American students so weak in problem-solving? Look no further than poor calculating skills.
Test prep limits content and prepares students to score better on a single test (?). But, test prep is not a coherent arithmetic curriculum and does not make students ready for higher math at future grade levels.
Inquiry/discovery learning (e.g., group work) is inefficient and not a practical pedagogy for learning mathematics or science.
Jumping up to critical thinking without first emphasizing the knowledge stage of Bloom's Taxonomy is a lousy pedagogy for mathematics. A bedrock of knowledge in long-term memory is required for critical thinking (i.e., problem-solving) in math or science or anything.
Common Core (CC) math standards were better than most state standards at the time they had been adopted, but, over the years, the new standards have not improved math achievement. Also, K-8 teachers did not have the math knowledge to teach the standards well (Dr. H. Wu). In short, Wu said that the new standards would probably fail. He should know! Wu has been giving courses and workshops for K-8 teachers for decades. They just don’t know enough mathematical content, which is the fault of the schools of education and their progressive professors.
Under CC, teachers teach less content to close gaps, which didn't work. CC promised to close gaps and "magically" remake kids college and career ready. Really? What does that mean?
In the real world, low achieving students in Common Core math and reading were not becoming high performing students who were college-ready, regardless of the funding from Gates and other sources. It was magical thinking by progressive reformists.
Schools continually appeal for more money to close gaps, which have become the chief mission of public education (often in disguise), but it shouldn't have been. (It still is!) In short, since the 70s, funding has mostly targeted low-achieving students, not the other students or the academically advanced. The funding was not for significant improvements in curriculum and teaching that would have benefitted all students. The crux is that we are not going to get better teaching or a better curriculum under the current "progressive pedagogical” system, no matter how much money is diverted to those goals. The educational elites in charge of education are not going to change.
We need more money for more technology in the classroom. More tech is the silver bullet. No, it is not!
The K-12 math curriculum and K-12 teaching need an overhaul, but the money went to gap closing, which is to low achieving students.
©2020 LT/ThinkAlgebra
©2020 LT/ThinkAlgebra
LT