Please excuse typos and errors.
For at least 50 years, progressive reformers have attempted to downgrade knowledge by attacking the teaching of tried-and-true traditional arithmetic, calling it obsolete and old school and branding it as poor teaching. The progressives have denigrated memorization and practice for mastery, which drive essential mathematical knowledge, both factual and procedural, into long-term memory for instant use in problem-solving.
It is what we have known down through the ages: Math knowledge in long-term memory fires up problem-solving, creativity, and innovation. In short, without knowledge ( i.e., lower level thinking), there is no higher-level thinking. Also, "It is pretty hard to understand mathematics without doing some mathematics," writes Professor Jordan Eilenberg (How Not To Be Wrong: The Power of Mathematical Thinking).
Note. The standard algorithm empowers students and requires automation of number facts.
It should be the primary method of calculation from the start of 1st grade, yet very few teachers teach traditional arithmetic, which has been shunned as "old school" and branded as "poor teaching." It's not true! The fact is that high-level thinking requires a solid foundation in low-level thinking, which is called knowledge. Kids can't do arithmetic unless they know some arithmetic--factual and procedural knowledge--in long term memory. Indeed, memorization and practice-practice-practice are essential for building a storehouse of knowledge in long-term memory needed for problem-solving. Memorization and practice are not obsolete, as some claim. They are essential and are firmly supported by cognitive science. It is important to acknowledge that memorization and practice-practice-practice build fundamental factual and procedural knowledge in long-term memory--knowledge that engages and enables problem-solving in mathematics, says Daniel Willingham, a cognitive scientist.
1. Jason Zimba, one of the two major writers of Common Core math standards, recently stated, "The standards also allow for approaches in which the standard algorithm is instructed in grade 1, and in which only a single algorithm is taught for each operation." I am a proponent of teaching the standard algorithm from the get go in 1st grade. Students are novices; they do not need a perfect understanding of regrouping or place value to use the grid. Understanding grows slowly. At first, only a functional understanding is needed. The standard algorithm is the focused goal for calculating and should be presented at the beginning of the school year. Traditional arithmetic when taught well works well.
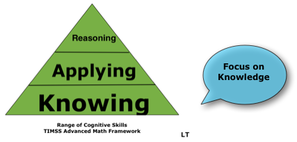 |
| Bloom's Taxonomy in TIMSS |
2. Tom Loveless writes, "Deeper Learning is the current term for an old idea. The notion is that schools spend too much time focused on the acquisition of knowledge, especially knowing facts. In the past century, several alternatives have arisen to dethrone the prominent role of knowledge in schools: project-based learning, inquiry and discovery learning, higher-level thinking, critical thinking, outcome-based education, and 21st Century Skills. Now it is deeper learning." Deeper learning has been yet another attempt to turn Bloom's learning taxonomy upside down and upend knowledge. According to the fundamentals of cognitive science, it is the lower level thinking (i.e., knowledge) that enables and fires up higher-level thinking, such as problem-solving, creativity, and innovation. Why are some educators continually trying to marginalize the prime importance and impact of factual and procedural knowledge in learning arithmetic well?
3. Kirchner-Sweller-Clark (Why Minimal Guidance During Instruction Does Not Work...) write, "Evidence for the superiority of guided instruction is explained in the context of our knowledge of human cognitive architecture, expert–novice differences, and cognitive load. Although unguided or minimally guided instructional approaches are very popular and intuitively appealing, the point is made that these approaches ignore both the structures that constitute human cognitive architecture and evidence from empirical studies over the past half-century that consistently indicate that minimally guided instruction is less effective and less efficient than instructional approaches that place a strong emphasis on guidance of the student learning process.” Students' desks are put together for group work and inquiry activities, which often use manipulatives. This configuration and minimal guidance methodology are not conducive to learning. The teacher is not the academic leader in the classroom. The teacher's role has been diminished to that of a facilitator. High-level thinking requires a solid background of low-level thinking, which is called knowledge.
4. Michael E.Martinez (Future Bright) writes, "Research supports a view of intelligence as both lower-order and higher-order. The mind's ability to engage in higher-level operations must in some way rest on a foundation of lower-level functions." This instructs teachers to focus on lower-order thinking first, that is, both factual and efficient procedural knowledge in arithmetic and algebra. Always remember, kids cannot operate on knowledge they don’t have.
✏️ Traditional arithmetic is tried-and true-and works well when taught well. But teachers coming out of schools of education have been taught to teach reform math by progressive-minded professors and to shun traditional [old school] arithmetic. Unfortunately, teachers are taught to discourage stacking numbers (vertical addition). They have been told that the standard algorithm is not an acceptable strategy, even though it is the "simplest, most efficient method for solving addition problems." Instead of traditional arithmetic, children are taught reform math strategies that use graphical methods (drawings) or counting and this (somehow) "magically" shows "deeper understanding," but it doesn't. The approach is often tedious, mostly unnecessary, and ineffective.
The reality is, kids can't do arithmetic unless they know some arithmetic (factual and procedural knowledge) in long term memory. And if they can't do arithmetic well, then they won't do algebra well, etc. Indeed, popular, minimal guidance instructional methods, such as project-based, problem-based, inquiry, discovery, constructivist, etc. are mostly ineffective and a waste of valuable instructional time. The popular methods are a mismatch to what most kids need, especially poor kids from single-parent households whose opportunities for success (i.e., catching up to the middle class) as adults are limited. Disadvantaged children, who come from one-parent households and are miseducated in schools will not have a shot at success. Poor children will become poor adults and dependent on government assistance programs. They will need more than ability and hard work.
Kids, today, need to learn more math than previous generations because high-tech jobs demand it.
On the other hand, memorization and practice are not obsolete; they are essential for putting necessary [key] knowledge into long-term memory. Students acquire number sense and become better at mental math because they have memorized number facts. In short, memorized facts enable students to become fluent in standard algorithms and better at problem solving.
Traditional Arithmetic
Get to the standard algorithm as quickly as possible.
In the early 80s, I gave a problem to my first-grade class in the first-month school. What is 32 + 37?
Background: Kids were already in counting exercises in the first full week of school and used cubes to measure, to count, and to work equations I made up. For example, I would write an equation on the board, such as 3 + 8 - 5 = box. The 3 means to put 3 cubes in the counting circle; the +8 means to add 8 more cubes in the same counting circle, and - 5 means to take out (remove) 5 cubes from the same counting circle. I circulated the room to make sure students were following the operations correctly. The box, which is a variable like x, means how many cubes are in the counting circle? After the three operations, the students would count the centimeter cubes in the circle, which is 6, so box = 6. The equations became more complex: 12 - 7 + 10 - 3 = x.
In a couple weeks, I gave them 31 + 27 = x. (Note. Kids started to memorize n + 2 addition facts. They also learned that adding 1 generated the next whole number: n + 1 = n'.) Kids were put in groups because there were not enough centimeter cubes to go around. (Note. By this time, students were used to breaking down numbers by place value. Thus, 31 was 3tens+1ones or 3t + 1 (We write ordinary numbers, such as 25, in positional notation.) The counting method describes above took a lot of time, and, often, the answer was not right. I asked students to do it again to see if they came up with the same answer. Some groups did, some did not. No matter, counting to add larger numbers was an arduous process for 6-year-olds. Counting is not an efficient method for adding and subtracting.
I wrote the following on the blackboard.
How did you do that? Students wanted to know! NOW! Remember the addition facts we started to memorize? I demonstrated how to do it by adding ones to ones and tens to tens, using memorized single digit math facts. It was a revelation to the students. There is a simple way to add, rather than counting cubes or making drawings, etc. We put away the cubes. And, so the standard algorithm was born. Place value is very important: the idea that 58 means 5tens 8ones or 50 + 8.
The standard algorithm empowers kids!
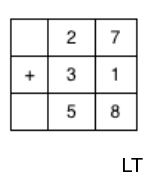 |
| A grid is helpful for some students. |
At first, explaining why something works is not as important as making sure students are competent at using the algorithm. To use the algorithm well, students need to automate addition facts. Students should master the algorithm without carry before proceeding to the carry concept.
Note. Children do not need perfect understanding to move forward. Understanding grows slowly. For example, Isaac Newton did not know why his calculus worked; it just did. (The conceptual understanding for calculus would not be developed for another 200 years.) However, Newton knew how to apply his calculation methods to solve physics problems. His calculus answers always matched the experimental values. In short, the calculus always worked.
An important addition application for 1st graders is to find the perimeters of polygons. Also, 1st graders should do a lot of word problems. They need to learn when the add, or subtract, or multiply (repeated addition) from word problems just like Singapore 1st graders.
Also, 31 + 27 = x is an algebraic equation and, therefore, follows the rule of equality, which states that the left side must be equal to the right side for the equation to be true: 58 = 58. Furthermore, to solve the equation, the student needs to do arithmetic. A numerical equation that shows the solution would be 31 + 27 = 58.
Word Problem: Jill has 31 pencils, and Jack gave her 27 more pencils.
How many pencils does Jill have now? Write an equation that shows the solution.
 |
| The equation is the model. |
Note. All these things require practice-practice-practice so they stick in the long-term memory.
©2015 LT/ThinkAlgebra.org

