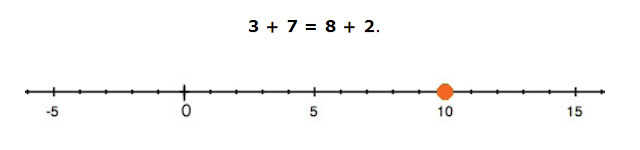Equation Notes

An Equation Is Like a Balance 

Teach students to "think like a balance" (left side = right side). An equation is a puzzle. The equal sign does not mean "calculate the answer." For example, in the equation 12 + 5 = ❏ + 8, box is not 17. First grade students should start with simple equations (e.g., 4 + ❏ = 7) and advance to harder equations: (❏ + ❏ + ❏) - 9 = 24), using the algebra rule for substitution. The equations should relate to the arithmetic facts being learned. With practice, primary students can solve equations in one unknown (❏ is a variable like x in algebra). 

Examples:
4 + 3 + ❏ = 20
4 + 5 + 12 + ❏ = 33

❏ + ❏ + ❏ - 9 = 24

(❏ + ❏) - 2 = ❏ + 5

Students should learn number properties and memorize number facts for automaticity. Number properties, such as the equality axioms, control how numbers work and are essential for understanding arithmetic. Young children should learn how numbers behave.

In arithmetic instruction, a competent teacher can integrate basic algebra ideas (e.g., variables, equations, equality, algebra rule for [variable] substitution, etc.) along with reasoning and “guess and check.” These ideas can be taught as first-grade students learn arithmetic facts and procedures. Furthermore, an equation approach is a powerful opportunity for students to practice arithmetic and do “number property” reasoning. The equations for 2nd and 3rd-grade students move up a notch in difficulty. For example, third-grade equations should include fraction ideas, multiplication/division, and multiple operations. Examples of equations in one variable at grade 3 level:

    ❏ + ❏ = 5
    ❏ x ❏ + 12 = 21 
    12 x 4 x ❏ = 12 
    ❏ ÷ 4 + 12 = 19. 


Examples of challenging equations at 3rd or 4th grade level:
(❏ x ❏) - (5 x ❏) + 6 = 0     (❏ x ❏) - (13 x ❏) + 22 = 0.


Commentary

These are notes on equations from ThinkAlgebra. They are like “cheat sheets” for parents and teachers. They will help you understand the background knowledge students should have, including auto fact recall. Students learn true/false statements, variables, equations, axioms (e.g., equality), conventions, and the algebra rule for variable substitution. Furthermore, students use reasoning and apply a “guess and check” strategy to find unknowns.


I cannot overemphasize the primacy of background knowledge in long-term memory, both factual and procedural. The key to learning is practice to mastery. Furthermore, understanding and problem solving are rooted solidly in background knowledge. Practice builds factual and procedural knowledge in long-term memory.

FYI: I taught these ideas to my 1^st graders, but the equations were easier. My first-grade students memorized the “Make 10” and “Doubles” in the first couple of months of school. This is not the usual order for learning math facts. “Make 10” and expanding numbers by place value (e.g., 13 = t + 3 or 10 + 3) are background knowledge for understanding place value. 

Two Notes

1. No calculators should be used in elementary school. 

2. Students in 3^rd or 4^th grade do not use algebraic methods for solving these equations. They used guess and check, math facts, procedures, conventions (order of operations), axioms (equality properties), the rule for substitution, etc.

Note: In 2016, I taught 4th-grade students to use inverse operations to solve one-step equations such as x + 5 = 12.  Students also solved two-step equations such as 3x + 5 = 32 using inverses. Using inverses is an algebraic technique.

The commentary below is for specific equation types that can be introduced at this level for prepared students; i.e., students who have sufficient background knowledge. There are prerequisite skills. Teachers with sufficient knowledge in mathematics can figure out what these skills are and teach them in a coherent manner.  

“Think like a balance” illustrates the transitive property of equality, which is the reason  “2 + 3 = 4 + 1” is a true statement (left side = right side or 5 = 5). The transitive property of equality, roughly stated, implies that if two things (2 + 3 and 4 + 1) are equal to the same thing (5), then they are equal to each other. Thus, 2 + 3 = 4 + 1. This is a “number property” approach to arithmetic. In short, both “2 + 3” and “4 + 1” name the same point on a number line, which is 5. The equivalency idea is fundamental in 1st-grade arithmetic, but it is seldom taught this way. 


The transitive property of equality is the reason that 3 + 7 = 8 + 2 is a true statement. Both 3 + 7 and 8 + 2 names the same point on the number line (10) and, therefore, are equal to each other: 10 = 10. 
  

Equivalency is also fundamental in fractions, ⅛ = .125, or  ¾ = 3 x ¼ = ¼ + ¼ + ¼, etc. Substitution of equivalent forms is a fundamental idea in arithmetic, algebra, trig, and calculus. 

Grade 3 Level Equations

NOTES/Draft 1 To Be Revised

1.  ❏ + ❏= 5

2. ❏ x ❏ + 12 = 21 

3. 12 x 4 x ❏ = 12 

4. ❏ ÷ 4 + 12 = 19. 

5. (❏ x ❏) - (5 x ❏) + 6 = 0 

   

The equation approach for practicing arithmetic and learning algebra ideas is challenging for students. Kids need a “cognitive” stretch to improve math ability. To match or surpass kids in other nations, young students should learn substantially more mathematics than is currently taught. 

An equation is like a balance (left side = right side), which is the equality concept. Students should learn to think like a balance. While these equations are for prepared 3rd-grade students, they can also be used in 4^th grade. I taught some of these ideas, such as the algebra rule for a substitution or the idea of thinking like a balance (left = right), to my 1st-grade class.  

Double Box: ❏ + ❏          (x + x or 2x)

Triple Box: ❏ + ❏ + ❏      (x + x + x or 3x)

The Box is a variable like x in algebra. A double box or triple box means the same variable (box). Thus, the same number must go in all boxes in an equation or expression. This is the algebra rule for substitution. 

Suppose the equation is ☐ + ☐ = 8. If we put a 3 in each box, then we would get 3 + 3 = 8, which is a false statement because the left side is 6 and the right side is 8 (6 ≠ 8). Think like a balance. If we put a 4 in each box, then we would get 4 + 4 = 8, a true statement (8 = 8). It is true because the left side (4 + 4) is equivalent in value to the right side (8). In guess and check, students find a number for box that makes a true statement. 

Let’s say the student places 5 in the first box and 3 in the second box, doesn’t that make 8? Well, indeed 5 + 3 = 8; however, the substitution for box is not allowed because box cannot be both 5 and 3 at the same time. In the equation ❏ + ❏ = 8, if you place a 5 in the first box, then you must place a 5 in the second box. If the equation were box + triangle = 8 or  ❏ + ∆ = 8, then box and triangle are two different variables, and each could be a different value or even the same value. Thus, one valid solution for the equation ❏ + ∆ = 8 is 5 + 3 = 8. In short, box is 5 and the triangle is 3. Another solution can be box = 4, triangle = 4, etc. Instead of ❏ + ∆ = 8, we write x + y = 8 in algebra. There are several whole number solutions to this equation, including 0 + 8 = 8, and an infinite number of “real number” solutions, such as 2.655 + 5.345 = 8, etc. 

Okay. In the first equation, ❏ + ❏ = 5, third-grade students might try whole numbers (guess and check). For example if a student tries 3, she gets 3 + 3 = 5, which is a false statement (6 ≠ 5). If she tries 2, she gets 2 + 2 = 5, which is a false statement (4 ≠ 5). Thus, the student should reason that the number that works must be between 2 and 3. (This idea can be taught in 2^nd grade, even 1st, if students have had experience with fractions and mixed numbers.) The answer is 2½ because 2 ½ + 2 ½ = 5. Another way to think about the double box is that the box must be half of 5. In short, split 5 into two equal parts. Students in 2^nd and 3^rd grade should have experience with fundamental fractions. It is called background knowledge, especially adding like fractions, the idea that ¾ is 3 x ¼ or ¼ + ¼ + ¼, and simple multiplication of fractions, including reciprocals. What is half of 5? (Sometimes, a number line with halves is helpful. Points between whole numbers are fractions. Thus, fractions, like whole numbers, are simply points on the number line. Thus, fractions are a logical extension of whole numbers.)

In the second equation, ❏ x ❏ + 12 = 21, students start with guess and check. The equation is a combination of multiplication and addition. Remind students that, by convention, multiplication is done before addition. This is part of the order of operations. If a student guesses 4, then 4 x 4 + 12 = 21, is a false statement. The left side (16 + 12) is 28, the right side is 21 (28 ≠ 21). So, 4 is too high. Try box = 3. Thus, 3 x 3 + 12 = 21, which is a true statement. The left side (9 + 12) calculates to 21 and the right side is 21 (21 = 21).

FYI: There is a second solution, which is -3. But the solution is ignored until students study negative numbers.  

In the third equation, 12 x 4 x ❏ = 12, the idea of reciprocal is important: n x 1/n = 1. Two numbers are reciprocals of each other if and only if their product is 1. (Again, this takes background knowledge. Students should practice multiplication of fractions that involve reciprocals. In short, we need to beef up content in 3^rd grade.) The student should reason that 4 x ❏ must equal 1 because 12 x 1 = 12, which is the Multiplication Property of One. Thus, 4 x ¼ = 1. Again, it is important for students to work with fractions and their reciprocals in 3^rd grade. FYI: The idea of “dividing by 2 is the same as multiplying by ½” is important in the division of fractions. 

In the fourth equation, ❏ ÷ 4 + 12 = 19, there are two operations, division, and addition. Children should be instructed that division, like multiplication, is done before addition (order of operations). Students should have an excellent grasp of their multiplication tables by Christmas in 3^rd grade. As in the other equations, students use guess and check and reasoning. Try box = 8. Thus, 8 ÷ 2 is 4, and 4 + 12 = 16, not 19, so 8 doesn’t work (16 ≠ 19). Try box = 12. Thus, 12 ÷ 4 is 3, and 3 + 12 are 15, not 19 (15 ≠ 19). Getting closer. Try box = 16. Thus, 16 ÷ 4 is 4, and 4 + 12 = 16. It is closer to 19, but the statement is false (16 ≠ 19). Try box = 28. Thus, 28 ÷ 4 is 7, and 7 + 12 = 19. Finally. 28 ÷ 4 + 12 = 19. True! The left side of the equation is 19, and the right side is 19 (19 = 19). Always think about balance: Left Side = Right Side 

Note Well. Instead of guess and check, another way to figure out the “number for the box” is to internalize (reason) that ❏ ÷ 4 must be 7 because 7 + 12 = 19. Thus, box is 28 because 28 ÷ 4 = 7. Students must know math facts. The more experience the student has, the better the student will reason in arithmetic. Showing students how this works is important. Students will need step-by-step practice with easier equations that lead to this equation. 

In the fifth equation (4^th grade), (❏ x ❏  - (5 x ❏)  + 6 = 0, start with guess and check as usual. This is a challenging equation for 3^rd, 4^th, or 5^th grade students. I used it in my 4^th grade class. Try box = 7. We get (7 x 7) - (5 x 7) + 6 = 0. The arithmetic is simple enough: 49 - 35 + 6 = 0, but 20 ≠ 0), so box = 7 doesn’t work. Too high. (Be sure to show how the arithmetic works. Also, remind students to do parentheses first, then subtract.) Try a lower number for box. Try Box = 4. We get (4 x 4) - (5 x 4) + 6 = 0, which is 16 - 20 + 6. How does a 4^th grade student handle this situation without getting into negative numbers? Simple. Add 16 and 6, which is 22, then subtract the 20. Thus, 22 - 20 = 2. But, 2 ≠ 0, thus box = 4 does not work. Continue guess and check until both solutions are found to (❏ x ❏) - (5 x ❏) + 6 = 0. They are not hard.

FYI: We can add 16 + 6 first because 16 - 20 + 6 is actually 16 + -20 + 6, which can also be rewritten as 16 + 6 - 20 (commutative property and definition of subtraction in algebra: 

a - b = a + -b). This explanation is not necessary at the 3^rd grade level. 

Practice equations like 12 - 14 + 6 = ❏, first. 

Before this, students should know what I call the “add in any order” property of addition, which I taught early in first grade. For example, to find the sum of  3 + 12 + 7, students recognize a “make 10” combination (3 + 7), add them first, and then add 12. Thus, 10 + 12 = 22, using mental arithmetic. Students should work extensively on “10 more than a number.” 

  

FYI: This equation is quadratic because box is squared. In algebra, the equation is written x² - 5x + 6 = 0 or y = x² - 5x + 6. By setting y equal to zero, the x values that work are the x-intercepts. Note the graph shape of the quadratic equation is a parabola. The x-intercepts are at x = 2 or x = 3. These are called the roots of the equation. 

I tell students there are two secrets. If you figure out the secrets, then you can look at the equation and figure out the two roots in 10 to 15 seconds. In the set of real numbers, quadratic equations can have zero solutions (no solution in real numbers), one solution (called a double root), or two distinct solutions.  

(❏ x ❏) - (2 x ❏) + 1 = 0

This equation has one solution (called a double root). The parabola intersects (bounces off) the x-axis once. 

I wrote quadratic equations in this form so that students can figure out two secrets. The idea is from the Madison Project. The equations are constructed so that the roots are integers. The idea of solving quadratic equations in this form in elementary school comes from the Madison Project, 1957. However, at this stage, the emphasis is finding the two secrets, applying the secrets, and practicing arithmetic.

There is a logical sequence of equations, step-by-step, that leads to each one of these five equations. Also, students should practice a lot. For additional information about equations, e-mail LT at ThinkAlgebra@cox.net.

LT

Visit my website: ThinkAlgebra

11-17-2010 Draft 1

Additional information added on 12-31-2010, 4-30-17

Number Properties

Numbers are abstract and difficult to define. 

Numbers are difficult to define, so use properties of numbers (axioms) to do arithmetic. Counting, which is a use of numbers, in an ineffective method to do arithmetic, yet counting and counting strategies seem to dominate U.S math programs in lower grades. While counting has its place, especially at the PreK and kindergarten levels, by 1st grade, we should focus instruction on the properties of numbers and the rapid acquisition of background knowledge (factual and procedural knowledge) in long-term memory. If you get the idea that the American approach has shortcomings, then you would be right. We do not teach arithmetic [or algebra] well. 

First-grade students should learn the properties of numbers, starting with equality and other properties of whole numbers [e.g., 0 is a whole number, zero property of addition (2 + 0 = 2), etc.], which, in turn, enable students to do arithmetic and, later on, algebra. Understanding implies “doing.”  Moreover, they should memorize the number facts and work extensively with operational procedures and axioms to build background knowledge needed for problem-solving. 

Understanding number ideas means knowing how numbers work (i.e., using number properties to make true mathematical statements: 5 + 0 = 5, 2 + 3 = 3 + 2, 12 = 10 + 2, 4 + 6 = 8 + 2, etc.  Doing arithmetic implies that students think in terms of making true statements. Furthermore, most number properties in basic arithmetic are simple ideas and easy to learn, such as the three equality properties of numbers: 5 = 5 (reflexive); if 10 = 3 + 7, then 3 + 7 = 10 (symmetric); and if 2 + 3 = 5 and 4 + 1 = 5, then 2 + 3 = 1 + 4 (transitive). (Incidentally, first grade students can verify number properties using cubes and equal-arm balances.) The same number properties apply to algebra. In first grade, I used words students could understand and told students to “Think Like A Balance.” An equation is like a balance. 

To learn more about number properties, see Endnotes 1 & 2. 

In arithmetic, algebra, and calculus, problem-solving is a function of prior knowledge and experience. To do arithmetic and other math well, at the least, requires the automaticity of facts and procedures; i.e., essential background [prior] knowledge in long-term memory. In short, the fundamentals of arithmetic and algebra should be taught for mastery but often aren’t. Unfortunately, the pace of math instruction in the United States is very slow, so it should be no surprise that our kids lag behind their peers from other nations. Our math programs lack rigor. Lastly, learning arithmetic and algebra well (mastery) takes repetition and lots of practice, yet practice has been out of favor in American classrooms for decades. 

Lastly, arithmetic is sequential (one idea builds on old ideas, etc.) and “the brain,” says John Medina (Brain Rules), “is a “sequential processor, unable to pay attention to two things at the same time.” In short, our brains thrive on a step-by-step hierarchy. (See “left/right brain bunk” below under Tangential Thoughts) Thus, arithmetic should be taught hierarchically to optimize the building of background knowledge, starting with number facts, number properties, and procedures. The focus in 1st grade should be on equivalent relationships and the number properties that govern them, rather than just counting. 

Find the number for box, so that (☐ + ☐) - 6 = 2.

My first-grade students worked equations like this but did not use algebra techniques. They used “guess and check,” reasoning, and knowledge; e.g., memorized facts and procedures, the order of operations (parentheses), conventions, equality axioms, and rule for substitution (variables). It takes time, repetition, and practice to reach this level. I started with very simple equations (e.g., 3 + ☐ = 7) and advanced step-by-step to more complex equations. Solving equations is one approach for students to practice math facts, algorithms, and number properties and to apply pre-algebra ideas (e.g., variable) and reasoning. Incidentally, box = 4 because (4 + 4) - 6 = 2.  When using x (instead of box) as the variable, the equation is (x + x) - 6 = 2 or 2x - 6 = 2. 

(See Endnotes 1, 2)

Draft 1 TBR Updated on 9-27-2010

Endnote 1

Find the number for box, so that (☐ + ☐) - 6 = 2.

If the right side is 2, then the left side must also equal 2 to make a true statement. Also, because the box is the same variable (☐ + ☐), then the number that replaces box must be the same number (rule for substitution). The purpose of solving an equation is to make a true statement (left side = right side). 

What is important for first-grade students is to apply the idea of equality. (THINK LIKE A BALANCE) This means the left side of the equation must be equivalent in value to the right side. In this equation, the left side = right side (2 = 2), if and only if box = 4, which is a unique solution; there are no other solutions. 

Introducing layers of difficulty through a sequence of equations is important, too. Here is another first-grade equation. In this example, the same variable is on both sides. All boxes must be the same number. 

(☐ + ☐) - 2 = ☐ + 5 

There are prerequisite equations to this equation, of course. Building to more complex equations takes time, persistence, repetition, and practice. My first-grade students did not use algebra equation solving techniques; they used “guess and check” and reasoning, along with memorized facts, procedures, axioms, rules, and conventions. Students were asked to think like a balance. Learning is based on repetition and practice. Knowledge in long-term memory is key to problem-solving. 

In (☐ + ☐) - 2 = ☐ + 5, box = 7 because 

      (7 + 7) - 2 = 7 + 5 

                   12 = 12. 

Note. In pre-algebra and Algebra 1, the equation is written 2x - 2 = x + 5. In short, an equation approach to arithmetic prepares students for real algebra they encounter in pre-algebra and algebra classes. Even though I did this in 1st grade as a means to practice number facts, properties, and procedures, elementary teachers in higher grades should find the ideas useful. 9-27-2010. (On 9-27-1905, Einstein introduced the mass-energy equivalence: E = mc².)

Endnote2

The properties of equality (equality is reflexive, symmetric, and transitive) and other properties are simple enough to teach to 1st grade students through practice and repetition, but this approach is seldom used in the United States, even though the properties of numbers provide a conceptual basis of “number” and help students understand how numbers work. For example, 12 = 10 + 2 is a true statement because the left side (12) is equivalent in value to the right side (10 + 2). Both “12” and “10 + 2” name the same point on a number line {12}. Therefore, they are equivalent to each other by the transitive property of equality, which roughly states that things equal to the same thing are equal to each other. If a = c and b = c, then a = b. Also, read First Grade Notes. 

The equal-arm balances my 1st graders used in the early 1980s came from a 1960s Science--A Process Approach (SAPA) module that I found in storage at district elementary school. (SAPA Equal-Arm Balance)