Math Grouping

Sort kids into homogeneous math sections by achievement, starting in 1st grade.

Arrange kids into homogeneous math sections by achievement. Don't worry about their self-esteem. Worry about their competency! 

Equal coverage of core math content is often confused with equal coverage of math content. While most kids can learn arithmetic basics and some algebra, many kids will not go on to learn trig or calculus. Let's face it; some kids are much better at math than others, and many are not being taught math they are capable of learning. 

Putting high achievers and low achievers in the same math class have been a recipe for underachievement and mediocrity. We have been mainstreaming kids for as long as I can remember. In a typical classroom, there is often a wide range of abilities or achievements in math. It means that the kids who learn math faster get bored and the kids who struggle stay behind. In my view, mainstreaming [inclusion] for math classes has led to underperformance at all levels. In short, the traditional system of heterogeneous classes for math is deeply flawed. Putting low achievers and high achievers in the same math class have hurt all our students because they are not challenged to learn the content they are capable of learning. Moreover, the "one-size-fits-all" common core reform math is not the answer. In addition, the popular instructional methods (minimal teacher guidance, inquiry, group work, etc.) are often less effective in teaching arithmetic and algebra. In my view, students underachieve for these reasons: the way students are grouped in math class, the math content taught (weak curriculum), the methods of instruction (ineffective), and teacher training (inadequate in math and science). [Note. In my view, common core is often driven by pedagogy leftover from the NCTM reform math it has replaced. More, later.]

Education creates inequalities. "In education, you increase differences. If someone's good at something, you try to develop his ability, which results in differences, or inequalities. So if education increases inequality, is this ethical?"  (Surely You're Joking, Mr. Feynman! by Richard P. Feynman.)  (First Draft. Please excuse errors. There are last-minute inserts.) 


Good education, says Feynman, should increase differences. The most realistic way to meet the diverse needs of most students in mathematics is homogeneous sectioning for weak students, average students, and advanced students. It is the most pragmatic means for upgrading all students to significantly higher levels of achievement. The sorting of students should be flexible and start early in the 1st grade. (Note. Kids enter school with differences, but US schools tend to ignore differences. In Singapore, differences are addressed, not ignored. In 1st grade, kids with weak number skills are pulled out for math periods and taught by a high-quality teacher. They are expected to learn core arithmetic just like the regular kids. The difference is these pull out kids are in a smaller class, instead of a class of 30, use different materials, and are assigned the best teacher. Most students catch up within a year because that is the goal, although the safety net program lasts through the 2nd grade.) 

The "many levels" in the same math class, an overemphasis on group work and inquiry learning, and minimal guidance methods have led to widespread underachievement and unintended consequences. In my view, the implementation of "many levels" in the same math class and a steady diet of group work do not define quality learning or excellence. Furthermore, educators seem caught up in a self-esteem mode rather than in a competency and achievement mode. Many students who get As and Bs in so-called "college prep" courses end up in remedial math courses at community college. We are told that common core math should eliminate the mushrooming remedial math problem, yet there is no evidence that it can. 

[Insert. Education is off the track because academic excellence has been replaced by a "fairness" mindset that equalizes downward and leads to widespread underachievement for all students. In addition, we need to switch from a "test culture" to an "achievement culture." The curriculum, which is taught in the classroom, is test-focused and narrow. In my view, the common core is an outcome of the fairness mindset and testing culture, which are interrelated. Common core math is not at the Asian level. Thus, US students start at a lower level and never catch up. Beginning in the 1st grade, math is not taught well. Nothing new. The math curriculum is weak, poorly thought out, and poorly taught. Standards (e.g., common core) are not the curriculum. The curriculum is what is actually taught in the classroom. Katherine Baird (Trapped in Mediocrity) says that too many teachers do not make good use of classroom time, which is one of the main themes of this post. One reason is that kids of uneven skill levels are in the same math class. She also states that most states define "proficiency" at low levels of competency. Professor Baird wonders why there are so few elementary schools that teach algebra and geometry? 

On ThinkAlgebra, I conclude that states should opt-out of the common core, adopt the Core Knowledge K-8 content and skills sequence, which is better than the common core, and allow individual schools to compose their own rigorous curriculum and achievement tests based on the students they serve. Note. Core Knowledge, not common core, sets up a coherent K-8 math sequence that prepares more students for Algebra 1 in 8th grade, which is the fundamental tenet of the National Mathematics Advisory Panel (2008) ]  

In reality, not all students will be high achievers. Kids vary widely in academic ability, motivation, persistence, effort, self-control, numbers, vocabulary, etc., yet we educators pretend that each student is the same, which is nonsense. We need to tackle the real world, not play with Utopian models. We create idealized models of reality (e.g., equality) then think they are a reality [William Byers], but every teacher knows some kids make little effort to learn things, many kids do enough to get by, and other kids just do not have the smarts.  Nevertheless, we bend over backward with money, time, and resources to make equality work. It just isn't going to work--it's not reality. We need a different recipe, one that works in the real world, not a fantasy.

The late Professor Feynman is right. In a sound education system, there will always be inequalities because education creates differences; however, the mixed group approach in place today is an unacceptable model because it has led to underachievement at all levels. And that's what many educators do not want to acknowledge. In short, our present system symbolizes [is code for] low-quality schooling. Kids need strong teacher guidance, a world-class math curriculum, a grouping that matches their achievement level, lots of practice to master math, and persistence. Instead, most kids get "minimal guidance" instructional methods (e.g., discovery, inquiry, group work, etc.), a weak math curriculum, mixed grouping in math class, and insufficient practice to automate fundamentals.

The road to equality is paved with good intentions, but it is easy to get stuck in the mud with good intentions because good intentions are not the same as good ideas that actually work. In fact, many of the ideas put into the classroom turn out to be bad ideas; e.g., kids must first have high self-esteem before they can learn. Wrong! Intellectual leaders in education have been wrong again and again. In education, inputs (differences like self-control, etc.) do affect outputs (learning). Kids come to school with sizable differences in academic ability and vast differences in vocabulary. You cannot equalize huge differences. The idea of "equalizing downward by lowering those at the top" [Thomas Sowell] is a "prevailing ideology" in education. It hurts kids. Unfortunately, says Sowell, high achievement is often equated with "privilege." Privilege, some say, is not fair! Sowell characterizes the progressive point of view this way: "Tests in school discriminate against students who did not study." Let's abolish tests and homework because some students, apparently the ones who study, delay gratification, and work hard, have an unfair advantage.] Note. Progressives, which have influenced education policies for decades, actually believe that utopia of equality is possible [Berezow & Campbell]. Get real.

Instead of giving each student the same, which is a fundamental premise of Common Core math [uniformity], we should bring students up to the level of mathematics they need to move forward and be successful in life. We are obligated as educators to give children opportunities as equal as possible and encourage students, regardless of background, to work hard to achieve and excel. We need more college-educated minorities and women, especially in the STEM fields. 

When content is taught explicitly, average kids can learn arithmetic and algebra at an acceptable level; however, weak-performing students should be in a math section that receives a double dose of instruction; e.g., KIPP 5th graders get 2 hours of math daily. Indeed, KIPP students spend more relevant time-on-task in mathematics in one day than some elementary students spend in one week. KIPP kids have longer school days, school on Saturdays, longer school year, and math homework. Advanced math students should be placed in a section that stresses depth, content acceleration, and rapid pace. Indeed, to move rapidly forward, the best math students, which often languish in the regular classroom, should be grouped together for math class. This is homogeneous sectioning for regular grades in elementary school and by course in middle school, e.g., pre-algebra or Algebra 1. It is time to bring back the "old school." Hey, I miss the chalkboards.

Homogeneous math sections should be taught by high-quality math teachers (not NCLB definition of highly qualified teachers). We don't have nearly enough high-quality math teachers. Furthermore, the grouping (low, average, high) should start in 1st grade. Weak kids in 1st grade should be pulled out for math class at the beginning of the school year. The best kids should be pulled out for math class, too. My algebra program helps identify young, mathematically able students.

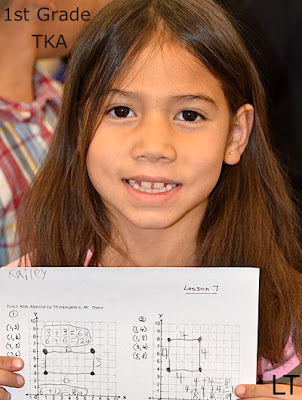Group the best 1st-grade math kids
for a daily pull-out class taught by
a high-quality math teacher.

Homogeneous Sectioning for ELEM Arithmetic; MS Pre-Algebra, Algebra 1 

1. Low performing students: (2C) double dose of core 

2. Average performing students: Core + 

3. High performing students: Core +++

Core denotes the knowledge and skills learned by average students in top-performing nations, e.g., Singapore. A good curriculum for US kids is Core Knowledge content and skills sequence, which is world-class and puts Algebra 1 in 8th grade. It does not refer to the common core. In short, Core means you don't dumb down the math. Elementary teachers must get better at teaching basic arithmetic. Moreover, the organizing of students should begin in 1st grade and be fluid up and down. Switching to homogeneous groupings and explicit teaching would be important progress, but it is not perfect. There is no perfect system, but there are systems that work much better than others. 

Students in three tracks end up at the same goal, which is to learn core. This would end "content incoherence," a term used by E.D. Hirsch, Jr. Kids need to learn core. The lower track learns core. The middle path moves faster and learns more than the core, and the advanced group soars way above grade level core. This is not equal coverage of math content; it is equal coverage of core.  

[Insert. Many middle schools offer some form of homogeneous groupings, such as advanced or honors-level classes in mathematics; however, this idea (honors math class) is rare in elementary schools because parents seem satisfied with math enrichment or with talented and gifted programs. The problem is that math enrichment does not move kids forward. Also, math enrichment is rarely taught by a high-quality math teacher. Consequently, some elementary school parents hire a private tutor or enroll their child in online courses from EPGY or Art of Problem Solving. In high school, students sort themselves; i.e., they can select from a range of math courses, including AP Calculus.] 

Decades ago, educators replaced the "old school" homogeneous sections (BAD) with a theory of equality (GOOD) that advocates mixed-level groups, self-esteem, group and project work activities, inquiry learning, grade inflation, less rigor, etc. Subsequently, there has been a steady decline in academic rigor in math, science, and other academic subjects. The outcome has been "massive underachievement" [Janine Bempechat], an epidemic of grade inflation, a glorification of "group work" that downplays individual achievement, and an explosion of remedial math classes at community colleges. In short, math achievement has stagnated over the past 30 years. What's more, memorization and practice, which are needed for the mastery of fundamentals of arithmetic and algebra in long-term memory, have fallen out of favor in many classrooms.

[Insert. There is a direct link between knowledge in long-term memory and the child's ability to solve math problems. Mathematicians have pointed out repeatedly that there is an intrinsic fusion between knowing the basics of mathematics in long-term memory (arithmetic, algebra, trig, etc.) and the quantitative reasoning skills needed to solve problems in mathematics. Prior knowledge is essential for problem solving and insight. Indeed, as Dr. Art Markman (Smart Thinking) points out, "Memory is all about connections." In mathematics, connections are vital because one idea builds on another. Everything fits together logically. To free "mental space" for problem-solving, math facts and efficient procedures need to be practiced, so they become automatic (mastery). There are no shortcuts. In spite of this, many US educators think the mastery of math facts, procedures, and skills are not that important.]

The replacement game plan of putting kids of mixed knowledge and skills in the same math classroom (inclusion policy) has not worked well. It does not make sense for a teacher to have several math levels in her elementary classroom. The teacher barely has enough time to plan for one good math lesson a day, much less several different math lessons, plus the reading groups and everything else. Consequently, quality instructional time-on-task at each math level has been limited and leads to underachievement at all levels. A lot of instructional time is wasted.

The idea of homogeneous sections is not perfect, but it is far better than what we have today, which are mixed-level classrooms and an almost impossible task of differentiating instruction in those classrooms. Consequently, many students, especially our best kids, go unchallenged and underachieve when compared to their peers in other nations. In a mixed group of students, while the teacher is working with one small group of students for 15 to 20 minutes (groups rotate), the teacher also has to classroom manage the other students, who are often distracted (talking, off-task behaviors, etc.) because they sit at desks in groups. In reality, students don't learn as much as they could or should and have less relevant time-on-task. FYI: In many of today's classrooms, the emphasis is more on improving group scores on the state math tests than on individual achievement. We are off-target.

[Insert. All children need challenging content, especially in math. For example, the content I introduce to little kids in Teach Kids Algebra (TKA) is difficult before it becomes easy. It is more difficult for some than for others. The "difficult" becomes easier a little at a time through memory, persistence, and practice--not group work. Indeed, success is a function of perseverance and hard work.] 

An attempt to make math classes [sections] more homogeneous is often met with harsh opposition because homogeneous grouping conflicts with [progressive] equality dogma. To "boost low-performing students," content has been weakened by subtracting core rigor.  States have lowered "proficiency" cut scores on NCLB math tests so that more students pass. Consequently, many students have been labeled "proficient" in state NCLB math tests, yet they do not meet the proficiency level in NAEP tests. 

Many kids, especially academically gifted students, go unchallenged in elementary and middle school and underachieve. It is caused not only by a weak math curriculum but also by mixed math classes. This "unthinking pursuit of equality" hurts all kids, explains Jacob Vigdor (Education Next, Winter 2013). The paradigm of subtracting rigor does not move students forward toward algebra in middle school. Indeed, it delays the math development of all students suggests Vigdor. My observation is the same. For example, 3rd-grade students who are not required to memorize multiplication facts for auto recall or practice the standard algorithm (x) for fluency are stalled. They cannot do long division, fractions, pre-algebra, or algebra. 

Subotnik, Olszewski-Kubilius, & Worrell (Scientific American Mind, November/December 2012) point out, "Today researchers, policymakers, and teachers pay little to no attention to high-achieving students ... Many such students spend their days in schools unchallenged--relearning materials they have already mastered." Students who are behind never catch up because that is not the goal. Our lower-skilled kids might get better in mixed classes because the focus is on them (NCLB), but most kids who are above average, especially our best students, according to Jacob Vigdor (Education Next, Winter 2013), are not challenged and underachieve because "instruction is not tailored to their varying needs." Like me, Vigdor wants to reorganize math classes via homogeneous sections because the sectioning works for most kids: weak, average, high.  

Homogeneous grouping across grade levels or by courses is not a new idea; it is not necessarily innovative, but it meets the needs of the vast majority of students substantially better than the mixed-group classes often found in our elementary and middle schools today. The practice of homogeneous grouping across grade levels was banished because it didn't fit the progressive concept of equality. On the other hand, Jacob Vigdor argues that mixed math classes hold all kids back, and he is right. Like me, Vigdor advocates differentiation via homogeneous groups, not "many groups" within the same math classroom, which impedes all kids.  

[Insert. Elementary teachers do not hesitate to place kids into several groups by ability for reading or for math within their individual classrooms, yet many balk at splitting all the kids at a particular grade level into math sections based on student knowledge and skills (homogeneous groups). The idea of establishing homogeneous sections for math, for example, conflicts with a progressive ideology of equality and self-esteem.]

[Insert. Dr. Janine Bempechat (Getting Our Kids Back on Track) says our children grossly underachieve. She asserts, "We need to worry less about self-esteem and more about competence ... We need to expect much more from our children and challenge our children to confront difficulty [and work hard]." Dr. Bempechat points out, "We have become so consumed with worry over our children's self-esteem that we take pains to manufacture it." Moreover, Bempechat insists, "We need to stop protecting children from hard work and sacrifice in the name of happiness and self-esteem." 

Also, Bempechat says that we need to teach children "critical academic and life skills, which are the ability to persist in the face of challenges, to delay gratification, and to endure boredom." It is indeed unfortunate that "many in our society [including elite educators] look down on academic excellence."]

Technology has been cast as the new panacea because, according to ardent supporters, kids can learn at their own pace. Sounds great, but it has never worked. For example, Individually Prescribed Instruction (IPI) in the early 70s was a total flop! Often in education, grand ideas that failed in the past are repackaged and pushed onto schools as innovative and transformative. They are not. Furthermore, adaptive software, such as Success Maker, is no match for a high-quality teacher, no matter the grade level. The equality dogmatists would have you think that the solution to our math woes is kids sitting at a computer learning math at their rates, which would be the ultimate in differentiation. Sounds great! But, it has not worked in the past. Unfortunately, some good ideas were banished by the "equality" dogmatists. One good idea was homogeneous grouping (weak, average, advanced).

I think the sorting of students should begin in early elementary school. For example, in Singapore, weak math students are pulled out for math class at the beginning of 1st grade and placed with a high-quality math teacher to catch them up. We don't do this. Moreover, weak math students in Singapore are expected to learn the same core arithmetic that is taught in the regular class. 

Notes1. Jacob L. Vigdor (Education Next, Winter 2013) makes a comparable proposal about grouping students in math, and Doug Lemov (Teach Like a Champion) thinks teachers should put desks in rows, so students face the board to enable attention during explicit teaching. Both ideas conflict with current practice and conventional thinking. Kids don't learn math by group; kids learn math [by inference and counterexample] from teachers who know math and use explicit teaching methods. 

Dr. Eric Hunushek says, "Schools do have a big influence on achievement." But, as Hanushek observes, "[Low income] schools...aren't geared to making sure that these kids [mostly minorities] get really high-quality teaching. They get average teachers, which, on average, doesn't make up for a family background [vocabulary gaps, etc.]." I am retired, but, as a guest teacher. I go to a Title 1 elementary school and teach algebra to little kids (grades 3 to 5), all minorities, to show teachers that many kids can learn content that leads to Algebra 1 in middle school. The explicit teaching of content is often a mismatch to school district policies of desks-in-groups, group work, and collaboration. Kids are novices, not experts. In the real world, experts collaborate, often by email. Frequently, schools do not live in the real world; they live in a fantasy world. If we want kids to become future innovators, then they must first "become an expert" [in a discipline] writes Evangelia G. Chrysikou (Scientific American Mind, July/August 2012). "A solid knowledge base will allow you to connect remote ideas and see their relevance to a problem." She points out, "Working alone is usually the best way to come up with creative solutions."  

[Insert. In Teach Kids Algebra (TKA), I want kids to master content to form a solid knowledge base because the kids who know stuff (facts, procedures, axioms, apps, and ideas) in long-term memory will be successful. Also, TKA is independent of the district's gifted programs; however, it does help identify students who learn math faster, have more insights, and handle complex, in-depth material. To stretch and inspire able students, I formed 4th grade and 5th grade Honors groups that met once a week. It isn't enough time, but it is a start. Moreover, "In academics, so far only in mathematics do we have reliable ways to detect potential talent early on," writes Subotnik, Olszewski-Kubilius & Worrell (Scientific American Mind, November/December 2012).]

[Insert. The content I introduce in elementary school classrooms is mostly algebra (variables, equality, true/false statements, writing and solving equations, x-y table building, graphing, functions, etc.) and pre-algebra stuff (integers, fractions, formulas, etc.). I do not teach specific items on the state NCLB math tests, although, at times, there is some overlap. By blending algebra ideas with arithmetic, students are more likely to make the conceptual leap from the specific to the general.]

Notes2. In the past couple of decades, [NCTM] reform math disciples have substituted "cooperative group work" for explicit teaching, and school districts, under NCLB, have focused instruction and resources on average and below-average students, often leaving the academically gifted, advanced, and even above-average students unchallenged. Reform math has downplayed the auto recall of number facts and the practice of standard procedures for mastery in long-term memory--both stall student achievement. Even students who are below average are frequently not challenged in this system. It is the wrong approach. We know that a lot of practice solidifies essential factual and procedural knowledge in long-term memory for use in problem-solving [prior knowledge is needed for problem-solving and critical thinking in math and science]. Educators need to reevaluate and challenge their assumptions, but they often don't. For example, kids who are not required to memorize multiplication facts in 3rd grade and work with the standard algorithm for fluency cannot do long division, fractions, or algebra. They are stalled. Group work and collaboration are championed in our schools, not individual achievement and academic excellence. We are in a test mode and not in an achievement mode. We are off-target. Under common core, this will not change much. 

The US math curriculum (i.e., content taught in the classroom) and instruction (i.e., methods of teaching math) are not a good model. If our curriculum and methods of instruction were an exemplary model, then most of our kids would score substantially higher on NAEP government tests and be near or at the top internationally rather than in the middle (TIMSS). Incidentally, Singapore teachers do not put kids on computers to learn basic math. I think much of the technology and software used in US classrooms by students is a distraction, not a viable solution.

Also, nearly 50% of the 8th graders in several Asian nations, including Singapore, score at the "advanced" level on international tests compared to only 7% of US 8th graders (TIMSS). This indicates that classroom teachers and cram school teachers in Asian nations not only teach core but way above the core for able students.  

Thinking Out Loud. Even though there has been some improvement, especially among less-skilled minority students, rapid growth, such as that found in many other nations, escapes us. We remain stuck in the mud [of mediocrity]. There are exceptions. For example, Massachusetts came in 6th with a score of 561 in 8th-grade math. South Korea was 1st at 613 on TIMSS. And, while the curriculum (e.g., algebra) has become more accessible to average students to promote equality, many students are not prepared academically to handle it because they are products of a weak elementary and middle school curriculum and inadequate instruction. Students should not take algebra if they are not prepared, yet many schools push kids into algebra, ready or not. It's an epic mistake. 

Jacob Vigdor writes, "America's lagging mathematics performance reflects a basic failure to understand the benefits of adapting the curriculum to meet the varying instructional needs of students." And, the adaptation Vigdor strongly suggests is differentiating via homogeneous math sections, starting early in elementary school, not the "many levels" in the same math class that we have endured for decades. Differentiating via homogeneous math sections is old school, and it works for almost all kids--weak, average, advanced.   

FYI. Regardless of the rhetoric from common core defenders, the hidden intention of the common core is to homogenize math content (equalize downward). In short, common core math is not designed to catch our kids up to international math benchmarks, which is a reason I classify it in the framework of equality/self-esteem [progressive] ideology. In my view, the common core is the latest manifestation of a "once size fits all" progressive dogma. Furthermore, our math textbooks and instructional methods often unduly focus on understanding, which is difficult to measure, at the expense of competency, which is easy to measure. (Peter Hanley, redefinED 12-31-12, writes, "Common Core standards seek to prepare students to achieve 1200 on the SAT.... [Nevertheless], the average score for America's teachers has been about 1000.") Schools of education lack academic standards. I think there are a lot of good teachers out there; we don’t have enough of them. Schools of education have not been graduating high-quality elementary and middle school math teachers.  

[Insert. Math, such as memorizing times tables, isn't much fun until you get good at it, which requires effort, study, and practice. Once you get good at something, you like it better. Parts of math can be hard and frustrating. It is a giant step to go from the specific (using numbers) to the general (using variables). 

In the US, math is often taught badly. We know that learning fractions and long division well in early elementary schools prepare students for algebra in middle school. Researcher Robert Siegler, Carnegie Mellon University, writes, "Early knowledge of fractions and long division predicts long-term math success." ]  

This document is an abridged version of the original (12-25-12) with additions. It is frequently updated, revised, and tweaked almost daily. 1-27-13

The document is not an essay. Please overlook disjoint parts, awkward sentence structure, incorrect grammar, spelling, and many inserts.

Comments may be addressed to ThinkAlgebra@cox.net.
Model Credit (top of page): Remi, 5th grade
Note. In this document, the term "progressive" is used as defined by Alex B. Berezow and Hank Campbell in their book Science Left Behind. 

Return to my main website. Click ThinkAlgebra
©2013 LT/ThinkAlgebra/MathNotes